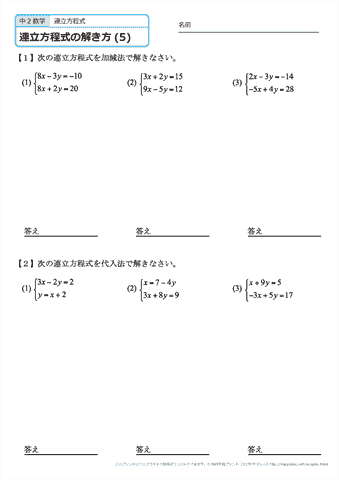
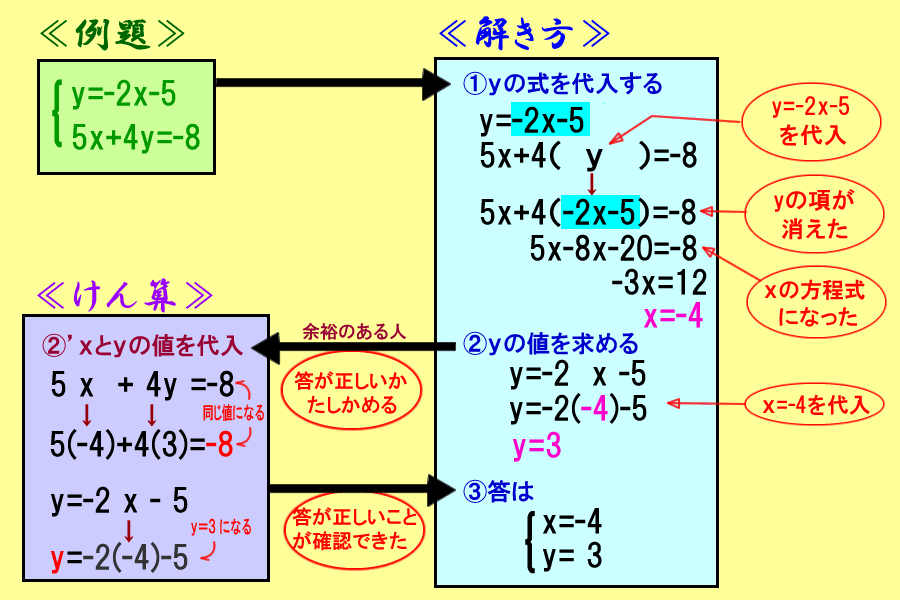
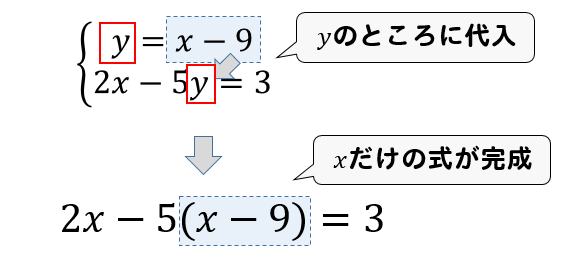
2つの式のどちらかが,すでにx=~またはy=~の形になっているときは代入法が 解きやすいです。 2つの式のどちらかのxまたはyの係数が1で,x=~またはy=~の形に変形できるときは 変形して代入法で解いてもいいですし,加減法で解いてもいいです。
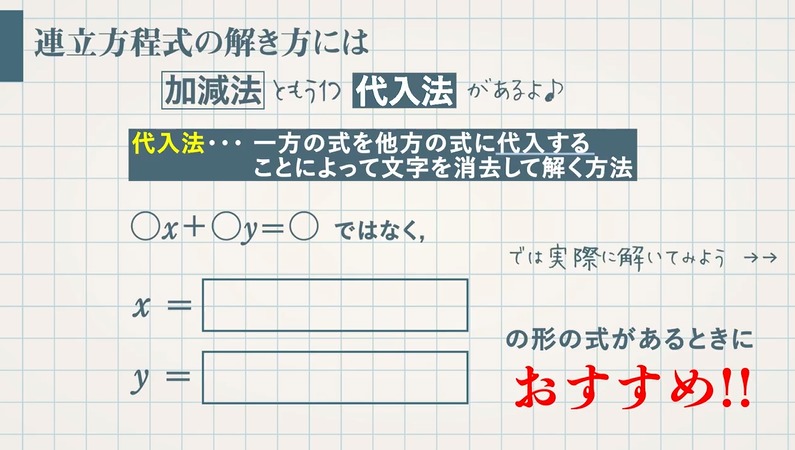
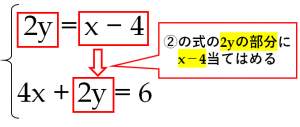
連立方程式解き方 代入法- 連立方程式の解き方 では、どのようにして解を求めるのでしょうか? 2つの方法を説明していきますが、共通するポイントを1つ。 文字を減らす これを意識して下さい。 1つの式の中に文字が1種類の時の解き方はもう学びましたね。 文字が1種類であれ連立方程式を解くには,xかyのどちらかの文字を1つ消去して,文字が1つだけの方程式にして解く。 この解き方に加減法と代入法がある。 加減法 x,またはyの係数をそろえて2つの式を 「たす」または「ひく」して文字を一つ消す。
連立方程式解き方 代入法のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
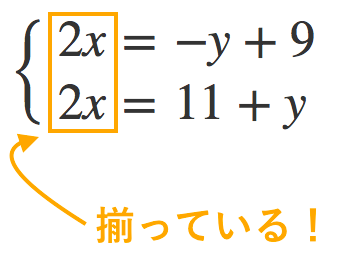 |  |  |
 | ||
 | 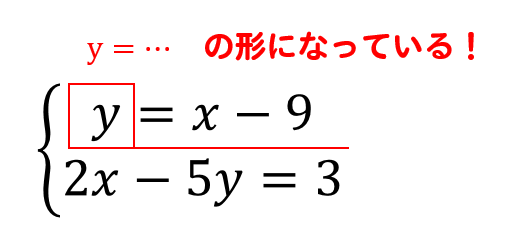 |  |
 | 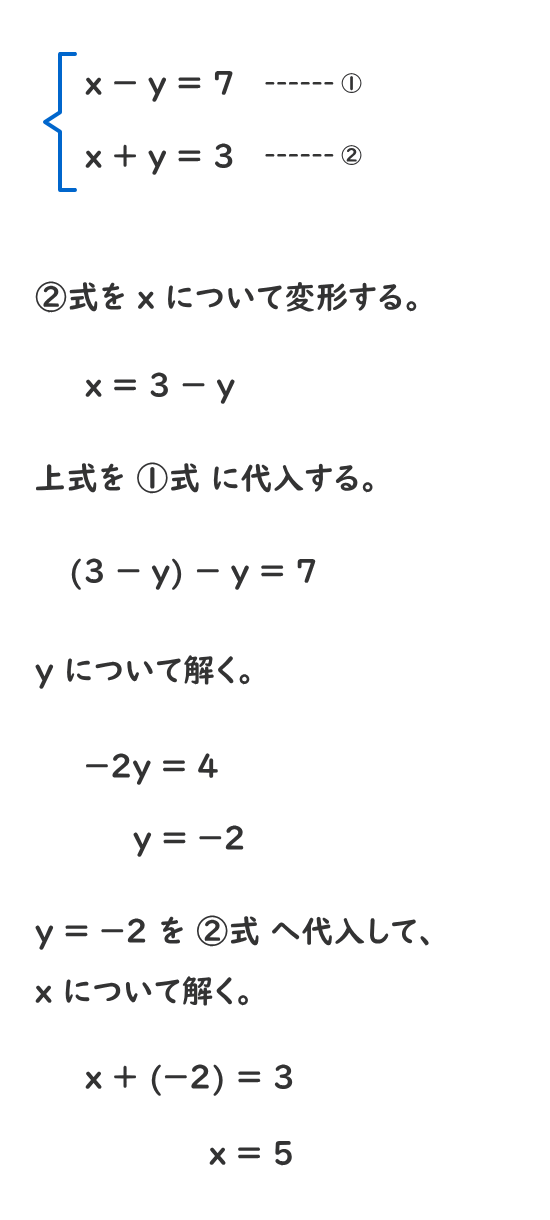 | |
「連立方程式解き方 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「連立方程式解き方 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
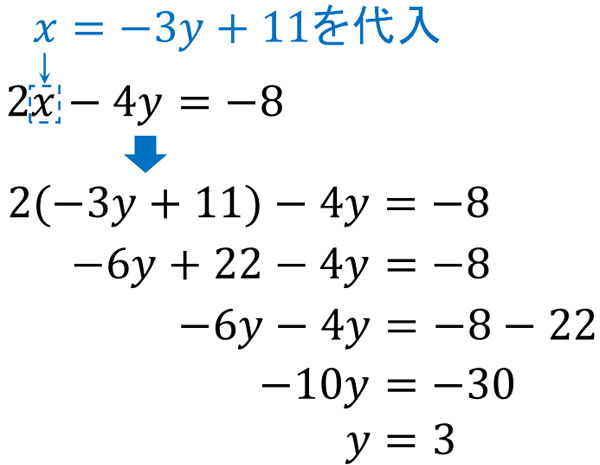 |  |  |
 | 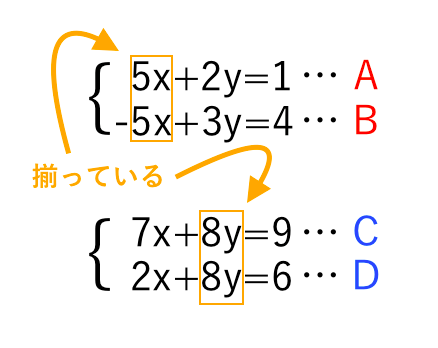 | |
 |  |  |
「連立方程式解き方 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | 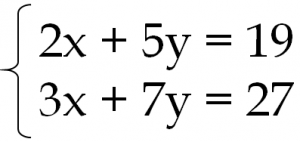 |  |
「連立方程式解き方 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「連立方程式解き方 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  |  |
「連立方程式解き方 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 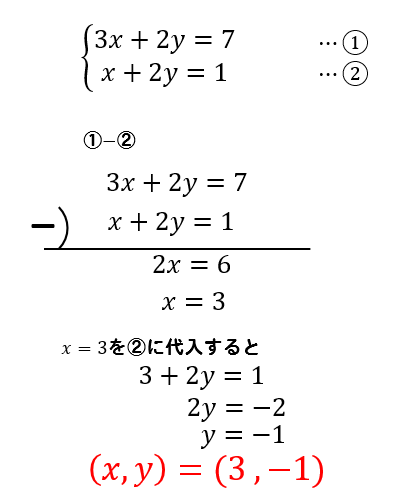 |  |
 | 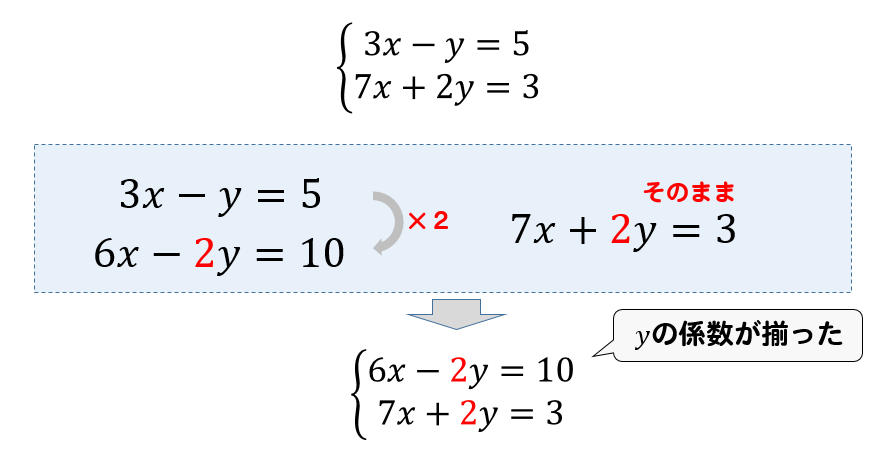 | |
 |  | 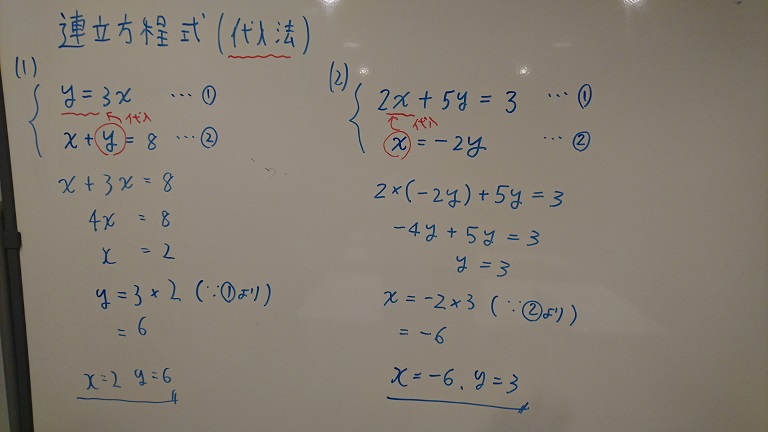 |
 |  |  |
「連立方程式解き方 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  | |
「連立方程式解き方 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
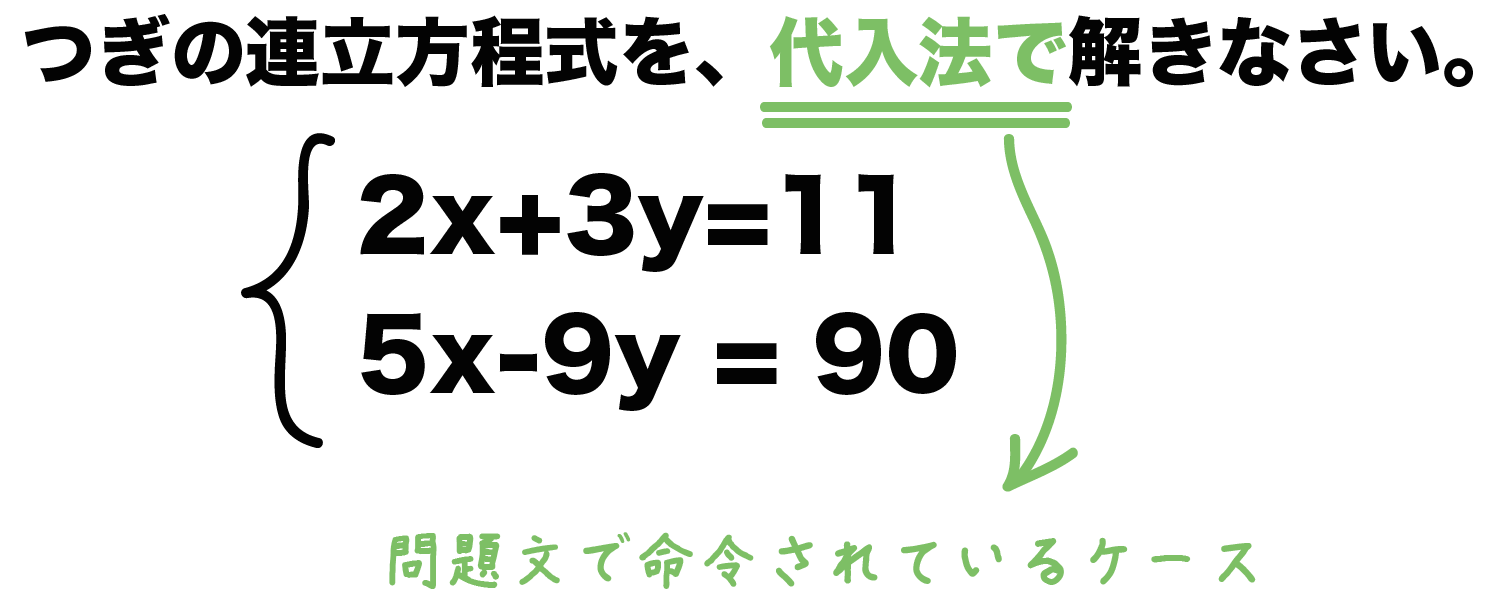 | 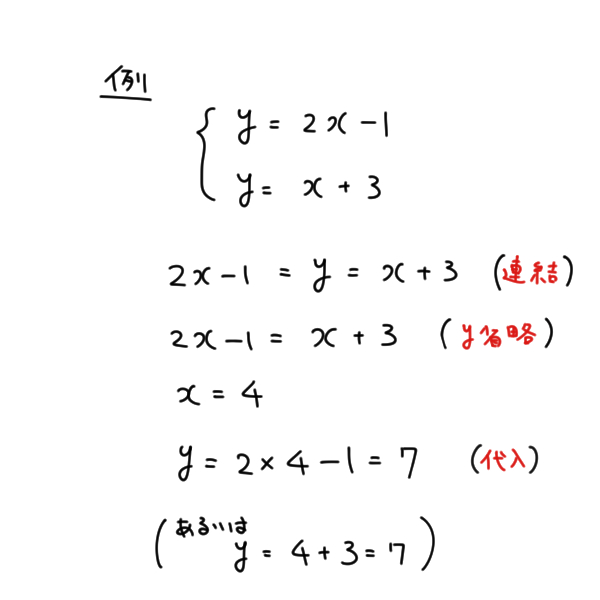 | |
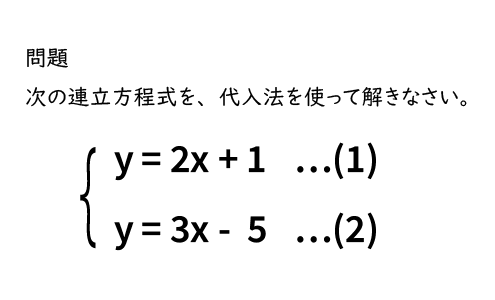 |  |  |
 |  |
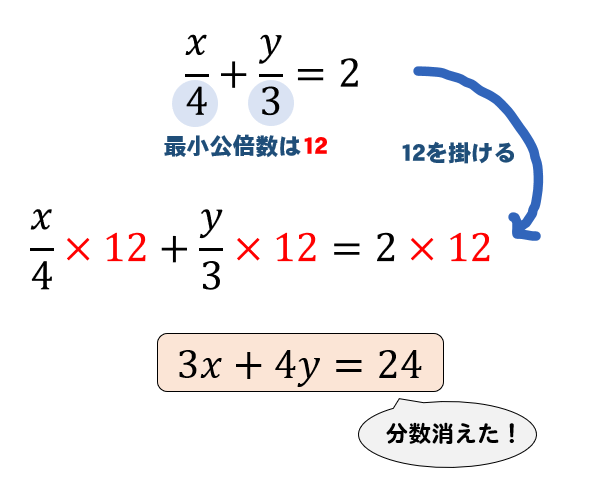
今回は連立方程式の解き方の一つである 代入法 について解説していきます。 代入法 は、 加減法 と同様に連立方程式を解く際に用いられる方法の1つです。 加減法でほとんどの問題を解くことが出来ますが、代入法を用いたほうがより早く、楽に解くこと 連立方程式の解き方でも紹介したけど、 迷ったら「加減法」をつかったほうがいいよ! だって、簡単だからね。 だけど、 ごくたまーに、 代入法が活躍するときもあるんだ笑 今日は、そんなときにそなえて、 連立方程式の代入法の解き方 を解説していく
Incoming Term: 連立方程式解き方 代入法,




0 件のコメント:
コメントを投稿